E-learning 2. Analýza dat 2.1. Obecný průběh analýzy 2.1.2. Porovnávání skupin (vyhledávání rozdílů mezi skupinami) 2.1.2.3. Regresní strategie
Regrese je silný nástroj, když je vhodně použita. Regresní analýza představuje sadu metod, které vyhledávají vztahy mezi závislou proměnnou a jednou nebo více nezávislými proměnnými. Studuje funkční závislost jedné proměnné na ostatních. Nezávisle proměnné se nazývají predikční nebo regresorové proměnné a značí se jako X. Závisle proměnná se nazývá vysvětlující proměnná a obvykle se značí jako Y. Regrese může u porovnání skupin zodpovědět různé otázky (znovu používáme příklad analýzy genové exprese):
- “Jak moc se změní genová exprese, když změníme hodnotu proměnné skupiny?”
- “Jak moc se změní genová exprese, když se změní hodnota nějaké další spojité proměnné?”
- “Jaká je pravděpodobnost, že vzorek náleží do jisté skupiny dané úrovní exprese genu?”
V první a druhé otázce je genová exprese závislá proměnná (predikovaná proměnná, výsledná), zatímco skupina (nebo spojitá veličina/proměnná) slouží jako nezávislá vysvětlující proměnná (prediktor). K zodpovězení těchto dvou otázek se používá lineární nebo nelineární regrese.
V prvním případě je prediktorem binomická nebo multinomická kvalitativní proměnná, v případě druhém je vztah mezi genovou expresí a nějakou kvantitativní proměnnou odhadnut. Vybrané příklady predikčních proměnných jsou sepsány níže:
- Binomické (se dvěma možnými hodnotami)
- Podtyp nádoru (AML, ALL)
- Odpověď na terapii (odpovídá, neodpovídá)
- Bakteriální forma (divoký typ, zmutovaný)
- Multinomické (s více jak dvěma možnými hodnotami)
- Podtyp nádoru (DLBCL podtypy: RARS, RCMD, RAEB1, RAEB2)
- Nejlepší odpověď na nádor (CR, PR, SD, PD)
- Bakteriální forma (divoký typ, mutant A, mutant B,...)
- Kvantitativní
- Doba přežití (celkové přežití, průběh samotného přežití,...)
- Hladina nějakého krevního markeru (....)
- Genová exprese dalšího genu
- Věk
Třetí otázka je zodpovězena pomocí logistické regrese. Oproti lineární regresi, slouží genová exprese jako predikční proměnná a výsledkem je proměnná skupiny.
Jak u lineární tak i logistické regrese mohou být vícenásobné predikční proměnné kombinovány. Například nás může zajímat odhalení odlišností genové exprese založených na nádorovém podtypu a věku pacienta. Nebo u daných hodnot exprese několika vybraných genů bychom rádi znali, jaká je pravděpodobnost, že má pacient jistý typ nádoru. Druhý případ je použit k sestavení prediktorů.
Nyní detailněji popíšeme lineární a logistickou regresi.
2.1.2.3.1. Lineární regrese
Lineárni regrese modeluje vztah mezi závislou proměnnou Y a jednou nebo více nezávislými proměnnými X tak, že nezávislé proměnné lineárně závisí na Y přes neznámé parametry, které musí být z dat odhadovány.
V našem příkladě Y reprezentuje vektor genových expresí ve všech vzorcích a X je matice hodnot vícenásobných proměnných (skupina proměnné, např. věk, podtyp nádoru, odpověď na léčbu). Přesněji, každé pozorování yi (hodnota genové exprese v jednom vzorku) závisí na pozorování proměnných xi_skupina, xi_věk,, xi_podtyp,, xi_odpověď přes střední hodnotu neznámých parametrů. Obecně, když uvažujeme p nezávislých proměnných a n vzorků, model (vztah mezi Y a X) je psán následně:

V našem příkladě p=4 (máme čtyři nezávislé proměnné: skupina, věk, podtyp nádoru a odpověď na léčbu).
Z toho důvodu je zde n rovnic (pro každé pozorování jedna), které mohou být psané formou vektoru:
 ,
,
kde Y je vektor pozorování závislých proměnných, X se nazývá matice plánu (design matrix), kde každý sloupec představuje jednu nezávisle proměnnou, β je vektor neznámých parametrů zvaných regresní koeficienty, které se pokoušíme odhadnout a ε je chybný člen nebo šum a zachycuje variabilitu všech dalších faktorů, které nejsou v modelu zahrnuty.
Hodnoty parametrů β1, β2,..., βp jsou samozřejmě stejné pro všechna pozorování (vzorky).
Pokud se rozhodneme použít tento model na naše data, musíme zkontrolovat následující hlavní předpoklady:
- Linearita vztahu mezi závislou a nezávislými proměnnými
- Normalita chybového členu
- Konstantní odchylka chyb (homoscedasticity)
- Nezávislost chyb
Pokud tyto předpoklady nejsou splněny, mohou být naše výsledky špatné a velmi zkreslené. Další velmi důležitý předpoklad je, že velikost vzorku n musí být větší než počet nezávislých proměnných p.
Nyní víme, co je lineární regresní model a jak získat nezkreslené výsledky, ale stále nevíme, jak odhadnout neznámé parametry β. Existuje několik metod k odhadnutí těchto parametrů, zde zmíníme nejjednodušší a velmi častou metodu odhadu zvanou metoda nejmenších čtverců. Tato metoda odhaduje β tak, že hodnota rozdílů čtverců mezi pozorovanými a odhadovanými hodnotami genové exprese je minimální:
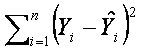 .
.
To je ekvivalentní s řešením následující rovnice
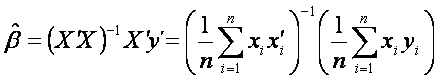 .
.
2.1.2.3.2. Logistická regrese
Jak již bylo zmíněno, někdy bychom raději zodpověděli otázku: "Jaká je pravděpodobnost, že vzorek náleží do jisté skupiny dané úrovní exprese genu?".
V takové situaci, kdy závislá proměnná je nominální nebo jinými slovy, když chceme predikovat pravděpodobnost výskytu události se dvěma možnostmi např. “nemocný” nebo “zdarví”, “muž” nebo “žena”, pak nemůžeme použít lineární regresi, protože taková nominální-váha proměnné nepochází z normálního rozdělení. Raději se používá logistická regrese. Může být také rozšířena na případy, kde závislá proměnná má více než dvě možné kategorie.
Logistická regrese je založena na logistické funkci, která je definována jako
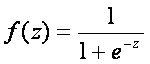 ,
,
Rozsah f(z) je mezi 0 a 1, a to je přesně to, co potřebujeme, protože logistický model odhaduje pravděpodobnost výskytu, který je vždy číslo mezi 0 a 1. K získání logistického modelu z logistické funkce píšeme z jako
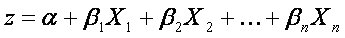
kde α je konstantní neznámý intercept (hodnota ze z bez nějakých rizikových faktorů), Xi jsou nezávislé proměnné zájmu a βi jsou konstantní neznámé parametry. Neznámé parametry jsou obvykle odhadovány pomocí maximální věrohodnosti. Každý z nich popisuje velikost kontribuce (podílu) jednotlivého faktoru. Pozitivní koeficient znamená, že faktor zvyšuje pravděpodobnost výskytu predikovaného jevu (vzorek náleží do skupiny), zatímco negativní koeficient znamená, že faktor snižuje pravděpodobnost výsledku. Čím větší je koeficient, tím je silnější jeho vliv na výsledek.