E-learning in analysis of genomic and proteomic data 2. Data analysis 2.2. Analysis of high-density genomic data 2.2.1. DNA microarrays 2.2.1.8. Analysis of arrayCGH

It is believed, that simultaneous searching for aberrated regions across samples from the same group can facilitate the search for group-specific aberrations.

One of the first approaches of this kind was proposed in [42]. The approach firstly applies the GLAD algorithm [20] to detect regions and to assign them one of the statuses normal, deleted or amplified. Results from this analysis are ordered into a matrix form where columns represent probes­, rows represent samples, 0 represents no aberration and 1 either deletion or amplification found in a position respective sample. Deletions and amplifications are treated in separate matrices. These matrices are further used for the detection of recurrent regions across groups. A recurrent region is defined as a sequence of altered probes common to a set of CGH profiles, and a minimal recurrent region (MAR) as a recurrent region that does not contain a smaller recurrent region (MARs). Two algorithms were presented to search for MARs, based on searching for blocks of probes with similar states obtained from GLAD across all samples. The first algorithm, MAR, efficiently computes all minimal recurrent alteration regions from a set of discretized profiles. The second algorithm, CMAR, allows to incorporate prior biologically relevant information such as a minimum frequency of a given alteration region in a dataset, or the number of observations defining the border of the alteration region and thus to minimize possibly too large numbers of MARs found by first algorithm. A kind of similar approach was introduced in [11]. The input data for the algorithm are in the same matrix form as in [42]. Then statistical testing is applied to search for consistent aberrations across samples. The null hypothesis is that the observed segments of aberration are equally likely to occur anywhere in the part of the genome being considered. The null distribution is obtained via random re-arrangements of the segments of each sample without replacement.

However, these approaches for the identification of recurrent regions are rather post-processing in nature than part of the segmentation procedure. Joint segmentation can prevent filtering out important signals present in the raw data. One of the first relevant approaches performing joint segmentation of the profiles across samples was proposed in [27] where the segment scores analysis is provided. The method is based on the assumption that under the null hypothesis no changes are observed in the data. The statistic amounts to

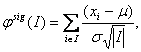
where I is a segment. It follows a normal distribution with m=0 and s² =1 for any I. Using this statistics a statistical significance is assessed for each segment. All the intervals whose statistics exceed a pre-defined threshold are considered to be putative aberrations. This one-sample case can be extended to the multiple sample case, allowing for two modes of analysis: fixed mode, where searching for aberrations present in all samples is performed, and class discovery mode, where searching for aberrations present in subsets of samples is performed. Engler et al. [13] suggested a three-state Gaussian mixture HMM model with parameters considered common not only across chromosomes but also across samples. They also introduced spatial dependence of the data and suggest performing classification based on posterior probabilities of states. Another joint segmentation approach was presented in [47]. This approach extends the single sample HMM model to the multisample case. Three methods are proposed: factored likelihood HMM, buffered factored likelihood HMM and hierarchical HMM. Shah et al. [47] report superior performance of the latter model. A further improvement of smoothing approaches for the analysis of arrayCGH data can be obtained by the introduction of a double heavy-tailed method due to [19]. It can be extended to the situation of multiple samples capturing group effects, performing joint parameter estimation.

Finally, a new method was proposed in [37] where the efficient segmentation approach of [35] is generalized to the case of multiple profiles. Their approach uses a mixed linear model with appropriate breakpoints. Model parameteres are estimated via maximum likelihood technique, obtained by the EM algorithm combined with Dynamic Programming (DP).