E-learning in analysis of genomic and proteomic data 2. Data analysis 2.2. Analysis of high-density genomic data 2.2.1. DNA microarrays 2.2.1.8. Analysis of arrayCGH

So-called segmentation methods attempt to divide the data into well-distinguished segments with different mean log₂ratios. The clones within an estimated segment are assumed to share the same copy number, and boundaries of segments are often referred to as breakpoints (or edges). Different estimation approaches are taken for the localization of the segments on the genome and the optimal number of segments.

Model-based segmentation techniques fit a model to the data and try to identify breakpoints in a manner that maximizes the likelihood probability distribution function. They can differ in the objective function and the optimization criterion used. The majority of these methods models the data according to a Gaussian process and performs the analysis for each chromosome separately.

Principle of model based segmentation techniques

To be more specific, let denote the measured log₂ratios for a given chromosome at positions 1…N, the main goal is to partition these values into segments … such that the copy numbers of the clones in each segment are identical. Indices where y₀=1 and y_k=N, represent positions of breakpoints (or simply breakpoints). The assumption is that for all x from the same segment the parameters of the Gaussian distribution are constant:

Because the clones are considered to be independent, the likelihood function can be defined as:

 

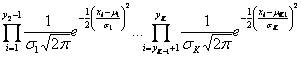
Maximization of this function according to leads to the estimation of an optimal partition of the data. This is equivalent to minimizing the logarithm of the negative likelihood function, what results into the sum of partial log-likelihoods:

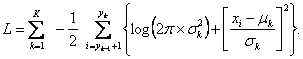
The search for optimal partition of the data (optimization) when K is known can be achieved by various algorithms.

Another task is to choose an appropriate K. Clearly, the higher the number of breakpoints (and so segments), the higher the value of the likelihood can be achieved. Thus, a penalty is required to prevent from overestimating the number of breakpoints. If we denote L_K the value of log-likelihood of the best partition of the data into K segments, then the optimal K can be estimated by minimizing the following equation:

where pen(K) is a function of parameters of the model such that the function increases with increasing number of parameters and b is a penalization constant. Table 1 displays various penalties that are used in arrayCGH analysis (based on [35]).

One of the first model-based segmentation approaches was proposed by Jong et al. [21]. A genetic local search algorithm is applied that finds the most probable partition of the data by minimizing the penalized maximum likelihood criterion. Picard et al. [35] assume a homogenous variance and fit the model via a dynamic programming algorithm. They points out that a constant penalty coefficient is likely to cause oversegmentation in a model and suggest an adaptative penalization criterion originally proposed in [25].

Table 1. Different penalty functions used in arrayCGH analysis.

criterion	b	pen(K)
AIC	1	2K
BIC	log(n)	2K
Jong et al. [21]	10/3	3K-1
Lavielle [25]	adaptative	2K

 

A slightly different and rather simple approach is taken in [33], a recursive segmentation technique, called circular binary segmentation (CBS). The main principle is the computation of a kind of Z-statistic that is compared to the value of theoretical distribution. This statistic is computed as follows: Let be the sequence of log₂ratios observed on a chromosome and let be the partial sums. Assuming a common known variance s² for all x_i, the Z-statistic is defined as, where Z_ij is the two-sample t-statistic for comparison of the mean of the observations with index from i+1 to j, to the mean of the rest of the observations:

Under the null hypothesis of no change, all Z_ij’s follow the normal distribution with zero mean and common variance s². A breakpoint is detected, when Z exceeds a a^th quantile of a normal distribution (or a permutation-based reference distribution). The process is repeated recursively in the detected segments until no change is found in any of inspected segments. The computational burden of their algorithm has been recently reduced to linear time in [52], where a hybrid approach for the calculation of the p-value of the test statistic and a new stopping rule has been introduced.

Another approach was proposed [30] based on a three-stage breakpoint detection algorithm. First, the edge detection filter consisting of a sequence of filtering steps is used for the estimation of locations of the breakpoints. Second, an EM-based algorithm is applied to provide fine-tuned adjustments to the breakpoint estimates. Finally, different statistical tests are performed to asses the significance of detected segments.

None of these algorithms comprise the assessment of the detected regions. The output of the segmentation methods usually consists of the breakpoints and the means of the segments. Segmentation methods thus need further analysis in order to classify estimated segments into biologically relevant states (deletion, normal, amplification).

 

GLAD

Hupé et al. [20] were among the first to address and implement this aspect. In their approach called GLAD, a local Gaussian regression model is assumed for each observation x_i:

The parameter q is estimated locally for each position via the adaptive weights smoothing (AWS) procedure [40]. When the parameter estimate for each clone is obtained, breakpoints are defined at positions where the q_i differs more than e=10^-2 from the q_i+1. The optimal number of breakpoints is then estimated via a penalized likelihood criterion which uses a tricubic kernel function. After fitting the model, a two step (chromosome and genome level) clustering procedure is applied for region assessment. The principle is as follows: at chromosome level, the data are clustered via hierarchical clustering with centroid criteria, taking into account the number of positions in each segment. Then the thus obtained dendrogram is successively cut down to obtain sets of clusters. The optimal number of clusters is selected again via a penalized likelihood criterion. This process is repeated at genome level with clusters selected at chromosome level. GLAD also pays special attention to the identification of outliers and their removal in each step of the analysis (both breakpoint detection and clustering).

Recently, Picard et al. [36] improved their segmentation method [35] by segmentation/clustering model. A dynamic programming-expectation maximization (DP-EM) algorithm is applied to alternatively estimate the breakpoint coordinates and the parameters of the mixture Gaussian model. Further, a heuristic technique for jointly selecting the number of segments and the number of clusters based on a penalized likelihood criterion is proposed. Another segmentation method taking into account the classification of the segments is due to Broët & Richardson [6]. Their method uses a Bayesian spatially structured mixture model and returns posterior probabilities for belonging to state k for each individual clone i. Similarly to the previous two methods, this technique applies also a classification procedure but a FDR estimate is proposed in addition. Both the classification procedure and the FDR estimate are based on posterior probabilities. In the work of van de Wiel et al. [51] several concepts of already proposed methods are combined. First, a CBS [33] is performed to segment the data, then random effects as proposed in [13] are applied and finally, a mixture model for segmentation results helps to obtain the most likely classification of segments. In order to follow the biological background of the data, the algorithm considers a six-state model, but the final classification which is based on rules derived from posterior probabilities, is set to three or four states.

A special contribution to the problem of classification of detected segments was contributed by Willenbrock & Fridlyand [55]. They proposed the method MergeLevels that performs a posterior analysis of data from the segmentation algorithms. The method merges estimated segments according to their mean log₂ratio values by combination of hypothesis testing (for wider segments) and thresholding (for segments with less than 3 clones). Two segments are merged if the distributions of the log₂ratios of the clones respective to these segments do not significantly differ or if the predicted level values are closer than the determined threshold. The procedure is repeated for increasing thresholds, and for each threshold the Ansari-Bradley 2-sample test [4] is applied to determine whether the distribution of the current residuals (current merged values minus observed log₂ratios) is significantly different from the distribution of the original residuals (original segmented values minus observed log₂ ratios). The optimal threshold is chosen as the largest threshold for which the Ansari–Bradley p-value is larger than 0.05 (where two types of residuals do not differ significantly).

A segmentation method focusing on analysis of SNP array-based data was recently developed in [56]. There, a two step method is applied for the identification of breakpoints. The first step is characterized by high sensitivity on the one hand and low specificity one the other, with the aim of identifying most of true breakpoints. This step is based on loess smoothing and the breakpoint is identified in the middle of each monotone part of a peak in the smoothed data, when the size of this part exceeds a pre-defined threshold. In the second step, statistical testing of mean log₂ratios of two segments around each breakpoint is used to remove false breakpoints. This testing is applied in a forward-backward algorithm, where an already removed breakpoint can be recovered if it is the most significant one among all the removed breakpoints and is more significant than the one just removed. Authors compare their technique to several other methods and report high sensitivity and high specificity in the detection of small copy number changes. This method seems to have the potential of performing well even when the data are very noisy.

MSMAD

Another segmentation approach of high computational efficiency, specifically designed to cope with very noisy arrayCGH data has been most recently proposed by Budinska et al. [7]. This method called MSMAD is rather simple and purely nonparametric, adopting a median absolute deviation concept for breakpoint detection, comprising median smoothing [12] for preprocessing. As the method is highly sensitive, the MergeLevels procedure should be used for post-processing to reduce the number of false breakpoints and to improve the final outcome by region assessment. One of the main advantages of this method is that the parameter specification in MSMAD is more intuitive and comprehensible than in many other algorithms, a feature which might be appreciated by users from outside the bioinformatics field. Yet another aspect of importance, this algorithm is suitable for very large data sets (resulting from new high density CGH arrays) because of its computational efficiency and moderate memory demands.